
The Information-Theoretic
Graphisomorphism-Algorithm
Graphisomorphism is one of the fundamental problems in mathematics as well as in complexity theory. Up to now (2009) it is not known, whether this problem belongs to P or NP.
Most practical algorithms for solving graphisomorphism relay on backtracking (VF/VF2 algorithm; see Amalfi Graph Database) or group theoretic approaches (see nauty). Unfortunately, these implementations are written in highly optimized C and therefore neither object-oriented nor user friendly.
Here we present a new fast graphisomorphism algorithm, called the Information-Theoretic Graphisomorphism-Algorithm (ITGI-Algorithm). It is written in object-oriented Java using the popular yfiles graph library. The ITGI algorithm can be freely downloaded here:

Information-theoretic Graphisomorphism Algorithm by Carsten Henneges is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 Unported License.
Permissions beyond the scope of this license may be available at www.itgi-algorithm.de.
This algorithm was first described in my diploma thesis "Algorithmen zur Graphmustersuche für das Netzwerkanalysetool BiNA", [BibTeX] [PDF].
Currently it is under revision at the Journal of Discrete Algorithms [www].
The algorithm is based on the observation, that a graph mainly consists of edges. Therefore it uses vertex-invariants, so called marks, to perform a computation that heavily relies on edges. In this way an intermediate graph representation is computed in which each edge (hopefully) had an impact. By first comparing these representations, which can be precomputed, many non-isomorphism candidates can be filtered out. When comparing graphs for equality, the precomputed marks aid the matching process. To initialize the computation, so called classificator functions assign marks each node of the graph depending on some general properties. The classificators are:
- the degree (Degree Classificator/DC),
- the connectivity degree (Connectivity Degree Classificator/CDC),
- the number of single nodes and length of the longest path (Longest Path Classificator/LPC),
- the LPC plus the cycle sizes (Single Nodes Longest Path Cycles Classificator/SNLPCC),
- or marks based on a BFS computation counting the number and size of cycles as well as the BFS depth (Breath First Search Classificator/BFSC).
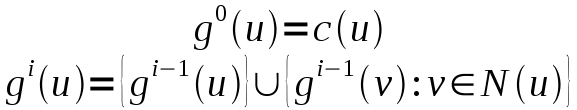
We found also counter examples where the first four classificators (DC,CDC,LPC,SNPCC) failed to yield good runtimes. These graphs were regular graphs wherein each node has the same degree. But the BFSC, which incorporates global properties, resulted in a good runtime, despite its expensive computation time.
Here is a little code snipplet to show, how this Algorithms is used:
---schnipp---
// Initialize the algorithm
GraphIsomorphyAlgorithm ga = new GraphIsomorphyAlgorithm();
ga.setGraphIsomorphyListener( ... ); // eventually register a listener for mapping events
// ga.setFastCheck(true); // compares only the intermediate representations
ga.setClassificator( new DegreeClassificator() );
ga.setDirected(true);
ga.setInitialize(true); // precompute represenations
// check this graph for isomorphism with the pattern graph; efficient if many graphs should be compared to this one musterGraph
ga.setMuster(musterGraph); // set a pattern graph
boolean isomorph = ga.check(hostGraph);
// alternatively
boolean isomorph = ga.check(musterGraph,hostGraph)
---schnapp---
If you have any problems running this algorithm, please write to help@itgi-algorithm.de.
Last update: 3 March 2010.